Problems tagged with "time complexity"

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    i = 0
    while i < n**2:
        i = i + 2
        j = 0
        while j < n:
            for k in range(n):
                print(i + j + k)
            j = j + 10

What is the time complexity of the following function in terms of \(n\)?

def foo(n):
    for i in range(n**2):

        for j in range(i):
            print(i+j)

        for k in range(n):
            print(i+k)

        for x in range(n - i):
            print(x)

What is the time complexity of the following function in terms of \(n\)?

from math import sqrt, log, ceil

def foo(n):
    for i in range(ceil(n**3 - 10*n + sqrt(n))):
        for j in range(ceil(log(n**2))):
            print(i, j)

What is the time complexity of the following function in terms of \(n\)?

def foo(arr):
    """`arr` is a list containing n numbers."""
    for x in arr:
        if x > max(arr) / 2:
            print('large!')
        elif x < min(arr) * 2:
            print('small!')
        else:
            print('neither!')

What is the time complexity of the following function?

import math

def foo(n):
    for i in range(math.floor(math.sqrt(n))):
        for j in range(math.floor(5*n**2 - math.sqrt(n)/1_000_000 + 100)):
            print(n * n)

What is the time complexity of the following function?

def foo(arr):
    """`arr` is an array with n elements."""
    x = max(arr) * min(arr)
    if sum(arr) > 10:
        return x
    else:
        return 0

What is the time complexity of the following function?

def foo(n):
    i = 0
    while i < n:
        j = 0
        while j < i:
            print(i + j)
            j += 1
        i += 5

What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n):
        for j in range(n):
            for k in range(n**2):
                print(i + j + k)

What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n):
        for j in range(n**2):
            for k in range(n):
                print(i + j + k)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(200, n):
        for j in range(i, 2*i + n**2):
            print(i + j)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

import math

def foo(arr):
    """`arr` is an array with n elements."""
    n = len(arr)
    ix = 1
    s = 0

    while ix < n:
        s = s + arr[ix]
        ix = ix * 5 + 2

    return s

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(n):
        for j in range(i):
            for k in range(n):
                print(i + j + k)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(n**3):
        for j in range(n):
            print(i + j)
        for j in range(n**2):
            print(i + j)

Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^3)\), while baz's time complexity is \(\Theta(n^2)\).

Suppose foo is defined as below:

def foo(n):
    if n < 1_000:
        bar(n)
    else:
        baz(n)

What is the asymptotic time complexity of foo?

The function below counts how many elements What is the time complexity of the following function in terms of \(n\)? Remember to state your answer in the simplest terms possible.

from math import sqrt, log, ceil

def foo(n):
    for i in range(ceil(n**3 - 10*n + sqrt(n))):
        for j in range(ceil(log(n**2))):
            print(i, j)

What is the time complexity of the following function in terms of \(n\)?

def foo(arr):
    """`arr` is a list containing n numbers."""
    for x in arr:
        n = len(arr)
        if x > sum(arr) / n:
            print('large!')
        elif x < sum(arr) / n:
            print('small!')
        else:
            print('neither!')

What is the time complexity of the following function in terms of \(n\)?

import math

def foo(n):
    for i in range(math.floor(math.sqrt(n))):
        for j in range(i):
            print(i + j)

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n**3):
        for j in range(n):
            print(i + j)
    for k in range(n):
        for l in range(n**2):
            print(k * l)

Suppose bar and baz are two functions. Suppose bar's asymptotic time complexity is \(\Theta(n^4)\), while baz's is \(\Theta(n)\).

Suppose foo is defined as below:

def foo(n):
    if n < 1_000_000:
        bar(n)
    else:
        baz(n)

What is the asymptotic time complexity of foo?

Solution

\(\Theta(n)\) If you were to plot the function \(T(n)\) that gives the time taken by foo as a function of \(n\), you'd see something like the below:

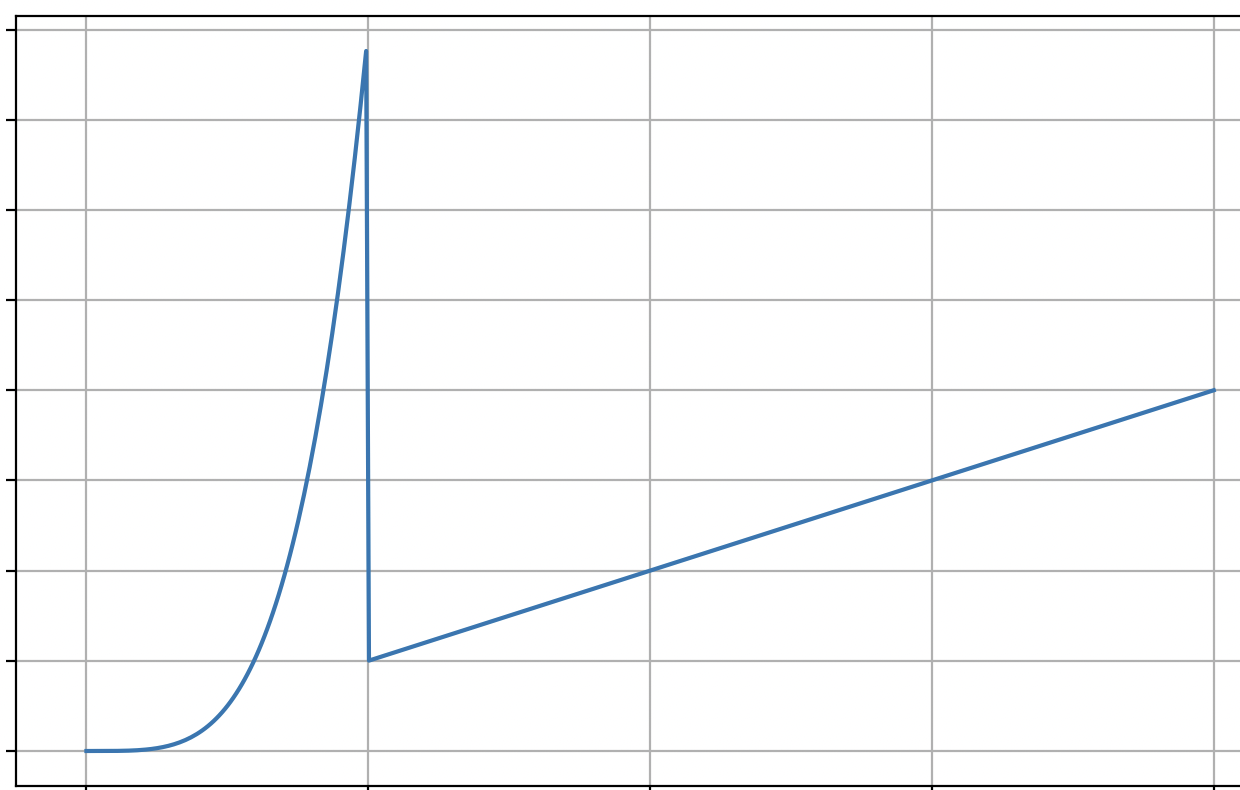
This function starts off looking like \(n^4\), but at \(n = 1_000_000\), it "switches" to looking like \(n\).

Since asymptotic time complexity is concerned with the behavior of the function as \(n\) gets large, we can ignore the part where \(n\) is "small" (in this case, less than \(1{,}000{,}000\)). So, asymptotically, this function is \(\Theta(n)\).

Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^2)\), while baz's time complexity is \(\Theta(n)\).

Suppose foo is defined as below:

def foo(n):
    # will be True if n is even, False otherwise
    is_even = (n % 2) == 0
    if is_even:
        bar(n)
    else:
        baz(n)

Let \(T(n)\) be the time taken by foo on an input of sized \(n\). True or False: \(T(n) = \Theta(n^2)\).